“Poter prevedere, sulla base di semplici misure a terra, il profilo verticale della velocità del vento fino a quote difficilmente raggiungibili con strumentazione dai costi contenuti è un evidente vantaggio, soprattutto nella fase di prefattibilità di un progetto d’impianto eolico”, spiega Giovanni Gualtieri dell’Istituto di biometeorologia del Consiglio nazionale delle ricerche (Cnr-Ibimet) di Firenze e autore dello studio. Questo compito è affidato ai modelli di estrapolazione della velocità del vento, la cui utilità pratica diventa oggigiorno sempre più stringente se si considera il costante aumento delle dimensioni dei moderni aerogeneratori, caratterizzati da un’altezza dei mozzi regolarmente al di sopra di 60-80 m, ma che arriva a superare (soprattutto nei modelli offshore) anche i 150 m.
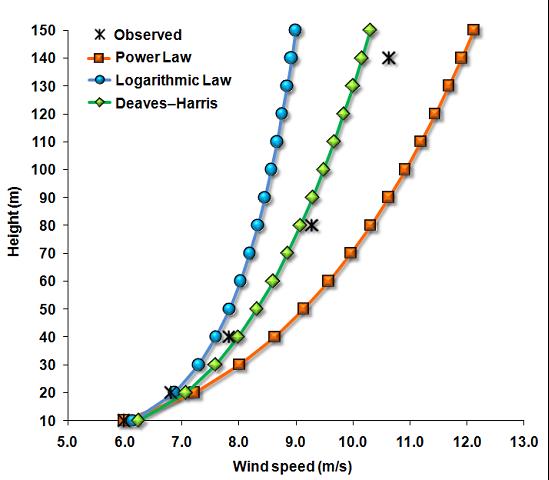
La ricerca, pubblicata su Renewable and Sustainable energy reviews, passa in rassegna 332 applicazioni condotte in un arco temporale di 40 anni (1978–2018) su 96 località nel mondo poste ad altitudini comprese tra 0 e 2230 m s.l.m.. Tre famiglie di modelli sono state prese in esame: (i) modelli basati sul profilo logaritmico; (ii) modelli basati sulla legge di potenza; (iii) modello di Deaves ed Harris. Il lavoro documenta l’accuratezza dei modelli applicati su ogni specifica località e ne discute nell’insieme l’andamento prendendo in esame quattro diversi tipi di sito: (i) pianeggiante e prevalentemente privo di ostacoli; (ii) collinare/ondulato con vegetazione/alberi; (iii) montuoso con orografia complessa; (iv) in mare aperto. Le prestazioni dei modelli sono state analizzate nella capacità di prevedere accuratamente il valore della velocità del vento in quota, ma anche nel riuscire a raggiungere quote particolarmente elevate, come richiesto dai moderni modelli di turbina eolica. “Oltre alla mera accuratezza numerica grande risalto è stato dato alla convenienza economica di un modello piuttosto che di un altro, e quindi alla strumentazione più o meno a basso costo richiesta per ogni applicazione”, evidenzia il ricercatore Cnr-Ibimet.
Tra i principali risultati raggiunti, lo studio evidenzia che i modelli basati sul profilo logaritimico (utilizzati in passato all’incirca nel 25.6% dei casi) risultano inadatti allo scopo, in quanto non in grado di raggiungere l’altezza tipica delle moderne turbine; essi presentano inoltre lo svantaggio di richiedere un’accurata stima della lunghezza di rugosità del sito (z0), cosa di norma alquanto complessa.
Per quanto concerne il modello di Deaves ed Harris, Giovanni Gualteri spiega che, nonostante sia utilizzabile a quote molto elevate (teoricamente lungo tutto lo strato limite), è stato finora applicato molto di rado (meno dell’1% dei casi), soprattutto perché richiede – oltre alla già citata lunghezza di rugosità – la conoscenza di un parametro abbastanza problematico come la velocità di attrito (u*).
I modelli basati sulla legge di potenza, infine, risultano quelli maggiormente utilizzati in letteratura (73.5%), sia per la loro semplicità d’impiego che per la loro affidabilità. “Essi non solo offrono una maggiore accuratezza nella previsione della velocità del vento in quota, ma riescono anche a raggiungere efficacemente le quote più elevate, tipiche delle moderne turbine”, conclude il ricercatore.